1. 탐색이란?
탐색은 '데이터를 찾는 방법'을 말한다.
여기서는 '어떻게 찾을까'와 '효율적인 탐색을 위해 어떤 방식으로 데이터를 저장할까'를 고민해야 한다.
정렬과 탐색은 정수를 기준으로 한다. 탐색할 데이터의 종류가 무엇이든 탐색 자체의 알고리즘에 대해서만 집중하기 위함이다. 따라서 데이터는 아래와 같이 구성한다.
typedef struct item{
int searchKey;
Data searchData;//Data : 원하는 데이터 type 적으면 됨
}Item;
2. 순차 탐색
- 단순하게 배열 처음부터 내가 찾는 값이 있는지 살펴본다.
- 정렬되지 않은 배열을 대상으로 함
- O(n)
3. 이진 탐색
- 배열의 중앙에 위치한 데이터와 비교해서 그 데이터보다 작으면 왼쪽 구역에서의 중앙값과 또 비교, 크면 오른쪽 구역의 중앙값과 또 비교해서 범위를 반씩 줄여나가며 탐색을 하는 알고리즘
- 정렬된 배열을 대상으로 함
- O(logn)
* 소스코드는 아래 링크를 참조하길 바란다.
재귀함수
1. 재귀함수란? - 함수 내에서 자기 자신을 다시 호출하는 함수 void Recursive(void){ printf("Recursive call\n"); Recursive(); } 2. 관련 문제 1. 피보나치 수열 #include int fibo(int n) { if (n == 1) retu..
yerinpy73.tistory.com
4. 보간 탐색(interpolation Search)
이진탐색의 변화 형태라고 보면 된다. '이진탐색'은 무조건 배열의 절반을 기준으로 탐색을 하는 반면에 '보간 탐색'은 찾는 데이터가 작은지 큰지에 따라 찾을 위치를 정한다.
'보간 탐색'은 데이터의 값과 그 데이터가 저장된 위치의 인덱스 값이 비례한다고 가정하고 있다. 그러므로 이진탐색과 마찬가지로 정렬된 배열을 대상하는 탐색 방법이다.
(찾는 데이터의 위치) = $\frac{x-arr[low]}{arr[high]-arr[low]}$ (high-low)+low
5. 이진 탐색 트리
연결리스트와 달리 2갈래로 나뉘어 찾아나가므로 결과적으로 살펴보는 데이터(노드) 수가 적어진다.
이진 탐색 트리에는 저장하는 규칙이 있고, 이를 이용하여 탐색을 한다. 규칙은 아래와 같다.
- 노드의 키 값은 중복되지 않는다.
- 루트 노드의 키가 왼쪽 서브 트리의 어떠한 노드의 값보다 크다.
- 루트 노드의 키가 오른쪽 서브 트리의 어떠한 노드의 값보다 작다.
즉, (왼쪽 노드) < (부모 노드) < (오른쪽 노드)의 규칙이 모든 노드에서 만족해야 한다.

6. AVL 트리
이진 탐색 트리의 시간복잡도는 O(logn)이다.
하지만, 트리의 균형이 맞지 않을수록 O(n)에 가까운 시간 복잡도를 보인다.

이 부분을 개선한 것이 AVL 트리이다. 'AVL 트리'는 균형 잡힌 이진트리라고 한다.
노드를 추가&삭제할 때 트리의 균형 인수를 보고 스스로 구조를 변경함으로써 균형을 맞추는 트리이다.
균형 인수 = (왼쪽 서브 트리의 높이) - (오른쪽 서브 트리의 높이)

AVL 트리는 균형 인수의 절댓값이 2 이상인 경우에 재조정을 하며, 종류는 4가지로 나눠볼 수 있다.
1) LL회전

루트 노드의 균형 인수가 +2인 경우 LL회전을 한다. left-left 회전을 줄여 LL회전이라 한다.
아래 그림은 위의 경우에서 더 확장한 경우를 보여준다.

서브 트리 T1~T4의 높이는 모두 동일하다. 그러면 서브트리의 높이는 8이 저장된 노드와 4가 저장된 노드의 균형 인수에는 영향을 미치지 않는다. 그러므로 위의 경우도 LL회전이 필요한 상태가 된다.
여기서는 서브트리 T3에 주목해야 한다. 4가 저장된 노드의 오른쪽은 8이 저장된 트리가 와야 한다.
그러면 T3은 어떻게 해야 하는가? 8이 저장된 노드의 왼쪽 자식으로 보낸다.
2) RR회전
LL회전과 방향만 다르고 원리는 같다.

3) LR회전
LR상태에서의 회전 방법을 말하며, LL상태나 RR상태로 바꾼 후에 균형을 맞춘다. LR상태에서는 RR회전을 통해 LL상태가 되게 하고 그다음 LL회전을 수행한다.
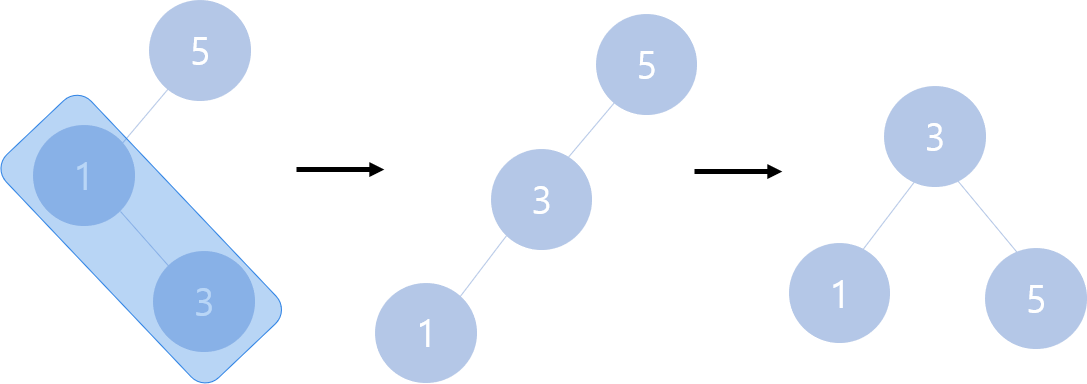
[STEP1] '3'이 저장된 노드의 오른쪽 자식이 NULL로 존재한다고 생각하고 '1', '3', 'NULL'을 RR회전한다.
[STEP2] LL 회전하여 균형을 맞춘다.
정리하자면 LR회전 = RR회전 + LL회전이므로, 서브 트리에 관한 처리는 LL회전, RR회전에서 설명했던 것과 같다.
4) RL회전
RL회전은 LR회전과 방향만 다르고 원리는 비슷하다. RL(상태에서의) 회전 = LL회전+RR회전

'CS > 자료구조' 카테고리의 다른 글
| 그래프(Graph) (2) | 2021.07.19 |
|---|---|
| 해쉬 테이블(Hash Table) (0) | 2021.07.16 |
| 정렬(Sorting) (0) | 2021.07.13 |
| 우선순위 큐(Priority Queue) (0) | 2021.07.11 |
| 트리(Tree) (0) | 2021.07.11 |